Praktische Anwendung und Auffinden der inversen Matrix

Die Matrix ist eine Tabelle, die gefüllt isteine bestimmte Menge von Zahlen in einer bestimmten Reihenfolge. Dieser Begriff wurde von dem bedeutenden theoretischen Theoretiker James Sylvester in Umlauf gebracht. Er ist einer der Begründer der Theorie der Anwendung dieser mathematischen Elemente.

Bis heute haben sie eine breite Anwendung gefundenbei der Durchführung verschiedener Berechnungen, die auf der Grundlage eines solchen Verfahrens aufgebaut sind, wie zum Beispiel das Auffinden einer inversen Matrix in verschiedenen Zweigen der menschlichen Aktivität. Diese Methode basiert auf der Bestimmung unbekannter Parameter des Systems verschiedener Gleichungen und wird häufig bei ökonomischen Berechnungen verwendet.

Es gibt die folgenden besonderen Fälle von Datenmathematische Komponenten: Kleinbuchstaben, Spalte, Null, Quadrat, Diagonale, Single. Der Kleinbuchstabe besteht aus nur einer Reihe von Elementen und die Spalte 1 besteht aus einer Spalte von Zahlen. Null - alle Elemente sind gleich 0. In einem Quadrat wie einem mathematischen Element entspricht die Anzahl der Spalten der Anzahl der Zeilen. Bei diagonalen Elementen, die sich auf der Hauptdiagonalen befinden, unterscheiden sich diese wiederum von "0", und der Rest darin sollte gleich "0" sein. Single - das ist eine der Unterarten der Diagonalmatrix. Sie hat nur "1" auf der Hauptdiagonale.

Beispiele für Matrizen:

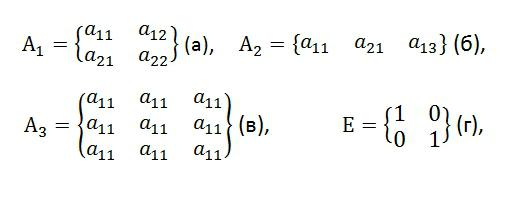
wo: A_k Ist ein allgemeiner Begriff, a_ij - Elemente,

(a) -2. Ordnung;

(b) - Kleinbuchstaben;

(c) -3. Ordnung;

(r) ist ein Beispiel für eine Einheitstabelle der zweiten Ordnung;

Auch hier gibt es eine inverse Matrix, die Definitionwas wie folgt ist. Wenn sie von der ursprünglichen Tabelle der Rückkopplungseinheit multipliziert wird, erhalten. Eine Vielzahl von Techniken, die die inverse Matrix ermöglichen finden. Die einfachste davon auf der Definition der Determinante basiert und Cofaktoren (manchmal auch bezeichnet als Determinante).

Die Determinante einer Matrix ist der Ausdruck a₁₁a₂₂-a₁₂a_21, es wird wie folgt bezeichnet: | À |. Die obige Formel gilt für eine Tabelle, die der zweiten Ordnung entspricht. Es gibt Formeln für Determinanten von Matrizen höherer Ordnung. Eine zwingende Voraussetzung für die Existenz einer Determinante ist, dass die Tabelle quadratisch sein muss. In der Praxis wird dieses Element dieser Theorie am häufigsten in einem solchen Verfahren wie dem Finden einer inversen Matrix verwendet.

Die zweite wichtige Komponente, durch die wir die Werte ihrer Elemente finden können, ist eine algebraische Ergänzung. Es wird nach der Formel berechnet: A_ij= (-1) ^ich+j * M_ij, wo M eine Minderjährige ist. Im Wesentlichen ist dies eine zusätzliche Determinante, die erhalten werden kann, indem die Zeile und die Spalte, in der sich das Element befindet, mental gelöscht werden. Zum Beispiel für eine Tabelle, die der zweiten Ordnung entspricht, die früher im Text gegeben wurde, für das Element a₁₁ Das algebraische Komplement ist das Element a₂₂.

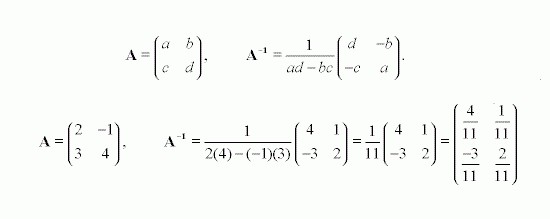
Die inverse Matrix wird in 3 Stufen gefunden. In der ersten Stufe wird die Determinante bestimmt. Im nächsten Schritt ergeben alle algebraischen Komplemente, die dann entsprechend ihren Indizes geschrieben werden, eine Tabelle algebraischer Komplemente. In der letzten Phase wird eine inverse Matrix erhalten, deren Ergebnis durch Multiplikation jedes algebraischen Komplements mit der Determinante endet.

Die am häufigsten verwendeten Matrizen sindDurchführung wirtschaftlicher Berechnungen. Mit ihrer Hilfe können Sie einfach und schnell eine große Menge an Informationen verarbeiten. In diesem Fall wird das Endergebnis in einer für die Wahrnehmung angenehmen Form präsentiert.

Ein weiterer Bereich der menschlichen Tätigkeit, inWelche Matrizen auch eine große Anwendung fanden - ist die Modellierung von 3D-Bildern. Solche Tools werden in moderne Pakete für die Implementierung von 3D-Modellen integriert und ermöglichen Designern, schnell und präzise die notwendigen Berechnungen zu erstellen. Der auffälligste Vertreter solcher Systeme ist Compass-3D.

Ein anderes Programm, in dem Werkzeuge für solche Berechnungen integriert sind, ist Microsoft Office und genauer gesagt eine Excel-Tabelle.

</ p>